Hola profe, espero se encuentre bien. Tengo una pregunta con respecto al ejercicio que realizamos ahora en la clase del turno de la mañana (10 a 13 h) de las Heras.
Los datos del problema eran:
μe = 0.4 μd = 0.2 m1=m2= 3 kg
a) Si m3 = 1 kg, y 1 y 2 se mueven juntos. Calcule la Fr entre ellos.
b) Calcule la m3max para que 1 y 2 se sigan moviendo juntos.
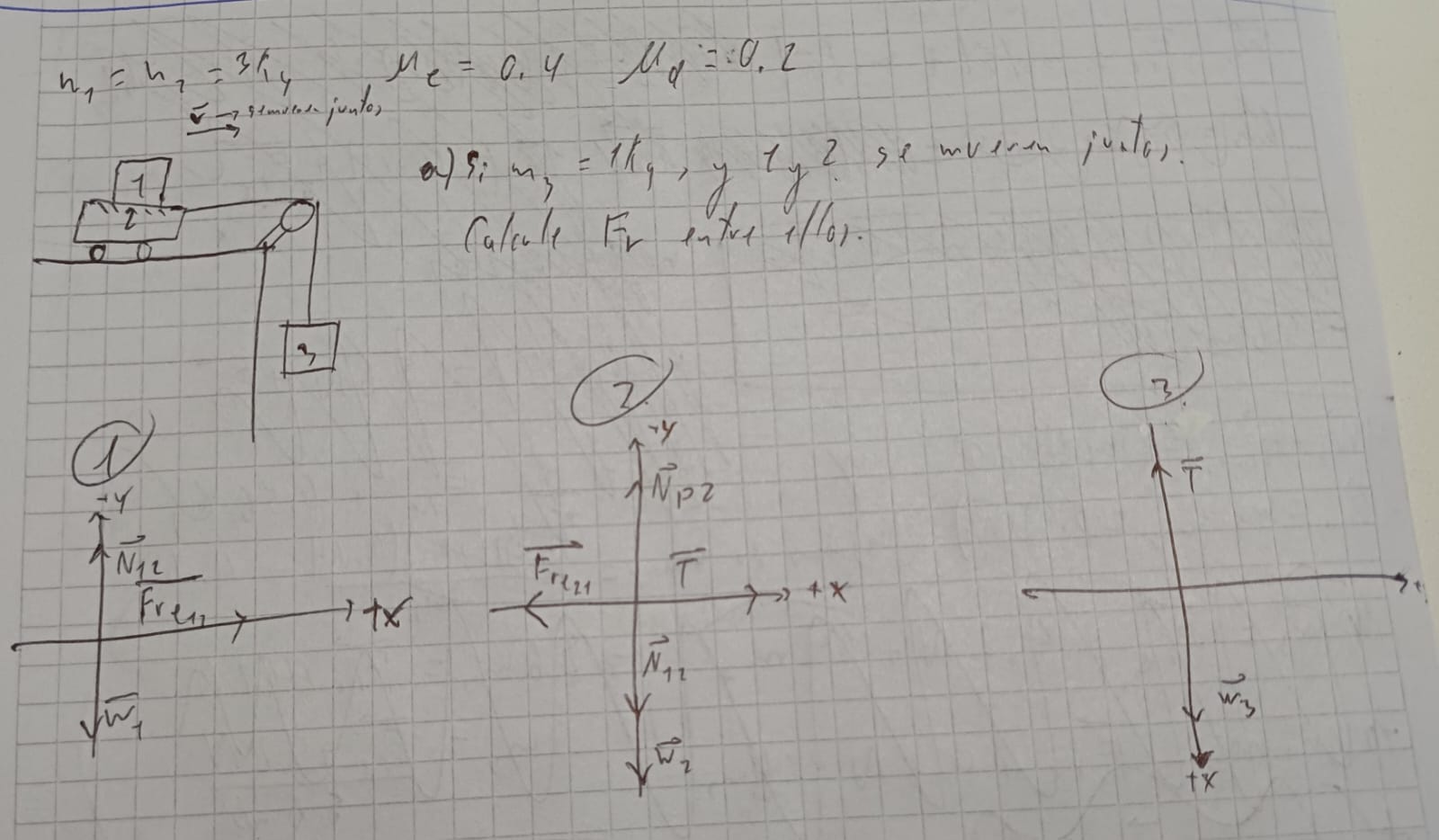
Mis preguntas son:
➤ Existe alguna manera de resolver el ejercicio tomando el sistema de referencia de la masa 3 con un eje y positivo hacia arriba y un eje x positivo hacia la derecha? En ese caso, las ecuaciones a continuación, ¿estarían bien planteadas con respecto al sentido de la aceleración?
Fre = m1*a ➊
T - Fre = m2*a ➋
T - P3 = m3(–a) ➌
➤ ¿Podríamos resolver el literal a) sumando las 3 ecuaciones de manera que nos quede: 2T - P3 = (m1+m2-m3)*a? Por que nos queda un termino de 2T? ¿Como podríamos deshacernos de el para llegar a la misma respuesta?
➤Para el literal b). ¿Como podríamos calcular la m3min para que 1 y 2 se muevan juntos? Podríamos plantear: 0 N < Fre <= Fremax ➝ 0 N < Fre =< (0.4)(30 N) ➝ 0 N < Fre =< 12 N
Para luego ocupar Fre = m1*a ➝ para mínimo (límite inferior): 0 N = (3kg)(a)min ➝ (a)min = 0 m/s2?
Y luego ocupar (a)min = 0 m/s2 con:
(m3)min*(10 m/s2) = (m2 + m3)*(a)min + Fre
➝ (m3)min = (3 kg)*(0 m/s2) + (m3)min*(0 m/s2) + 0 N donde Fre = 0 N porque ocupamos el limite inferior de la inecuación.
Y por tanto: 0 < (m3)min =< 4 kg donde 4 kg es el limite superior obtenido de la resolución del problema hecha hoy con usted.
Existe una manera mas sencilla de justificar el rango de masa 3 de 0 < (m3)min =< 4 kg?
De antemano le agradezco por su tiempo y ayuda. Quedo atento a su respuesta.
