Apunte: Dinámica de Cuerpos Vinculados

Leyes del movimiento de Newton, pilares de la dinámica, a través de ellas se generan las ecuaciones dinámicas del movimiento de cualquier sistema, que predicen el CAMBIO en el movimiento del sistema estudiado.   A saber:

Principio de inercia

"Todo cuerpo permanece en estado de reposo o de movimiento rectilíneo y uniforme, a menos que actúe sobre él una fuerza resultante no nula. Dicho en otras palabras: para que un cuerpo posea una aceleración debe actuar sobre él una fuerza no equilibrada"

Principio de la fuerza

"Una fuerza no equilibrada aplicada a un cuerpo le comunica una aceleración, de la misma dirección y sentido que la fuerza, directamente proporcional a ella e inversamente proporcional a la masa, m, del cuerpo"

Principio de acción y reacción

"A toda fuerza [acción] se le opone otra [reacción] igual y opuesta. Es decir, si un cuerpo ejerce una acción sobre otro, este último ejerce también una acción, del mismo módulo y dirección, pero de sentido contrario, sobre el primero. Estas dos fuerzas, aunque opuesta, no se equilibran mutuamente, ya que no están aplicadas sobre el mismo cuerpo. Las fuerzas de acción y reacción siempre están aplicadas a cuerpos distintos"

Guía sugerida en el procedimiento para abordar problemas que requieren la aplicación de las leyes de Newton 

• Dibuje un diagrama sencillo y claro del sistema.

• Aísle el cuerpo (u objeto) cuyo movimiento se analiza. Dibuje un diagrama de cuerpo libre para este objeto, es decir, un diagrama que muestre todas las fuerzas externas que actúan sobre él. Para sistemas que contienen más de un cuerpo, dibuje diagramas de cuerpo libre independientes para cada uno. No incluya en el diagrama de cuerpo libre las fuerzas que el cuerpo ejerce sobre sus alrededores.

• Observe que reconoce todos los pares de acción-reacción de interacción.

• Establezca ejes de coordenadas convenientes para cada objeto y determine las componentes de las fuerzas a lo largo de dichos ejes. 

• Aplique la segunda Ley de Newton, ∑F = m.a, para cada componente y cada cuerpo/objeto.

• Verifique sus dimensiones para asegurar que todos los términos tengan unidades de fuerza.

• Resuelva las ecuaciones de componentes para  obtener las incógnitas.

• Recuerde que se deben tener tantas ecuaciones independientes como incógnitas para poder obtener una solución completa.

• Verifique las predicciones de sus soluciones para valores extremos de las variables. Es posible que al hacerlo detecte errores en sus resultados.

Ejercicio de Cuerpos vinculados

Dos cuerpos de masa m_A = 5 kg y m_B = 3 kg están vinculados entre sí a través de una soga de masa ms=5 g, pequeña comparada con m_A y m_B. Se desprecia el rozamiento entre los cuerpos y el aire. 

Se tira del cuerpo A con una fuerza cuyo módulo es |F| = 1000 N.

a) Realizar el diagrama de cuerpo libre para cada cuerpo y para la soga.

b) Indicar cuáles son los pares de acción-reacción.

c) Si la soga es inextensible (la distancia entre todo par de puntos pertenecientes a ella permanece constante), calcular la velocidad y la aceleración de cualquier punto de la soga, y la velocidad y la aceleración de los cuerpos.

d) Para cada cuerpo, determinar el valor de cada una de las fuerzas actuantes y el de la fuerza neta o resultante.

e) Si ms → 0, ¿qué sucede con la fuerza que la soga ejerce sobre cada cuerpo?

DIAGRAMA DE CUERPO LIBRE                                                                  

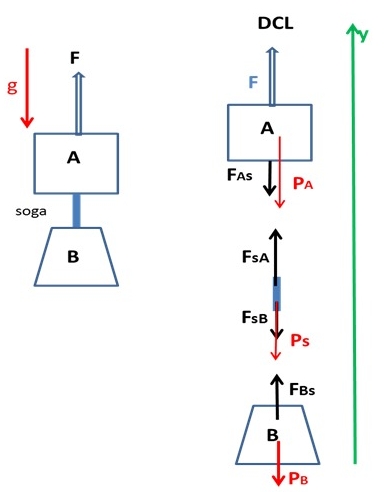
Desarrollo:

Denominamos a las fuerzas seg’un la siguiente convención:

  _{Sobre A <---}  F_{AS  --> ejercida por S}

Cuerpo A)   eje y)  F -   F_AS   - P_A = m_A  a_Ay     (I)

Cuerpo S)   eje y)  F_SA - F_SB   - P_s = m_s  a_sy     (II)

Cuerpo B)   eje y)          F_BS   - P_B = m_B  a_By     (III)

Consideraciones

1) F_SA  = F_AS     por ser pares de acción reacción (par).

2) F_SB  = F_BS     por ser pares de acción reacción (par).

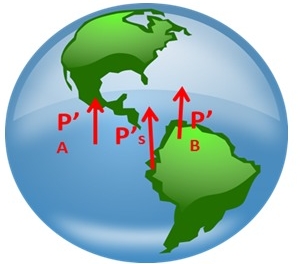
3) El par del peso de cada cuerpo está ubicado en la Tierra, dado que la fuerza peso es la fuerza (de interacción gravitatoria) ejercida por la tierra sobre el cuerpo en cuestión. Si quisiésemos seguir nuestra notación escribiríamos:

      P_A = P_AT   y  P’_A= P_TA   ídem para S y B

               P’_S= P_TS   y  P’_B= P_TB

4) ¿Qué relación guardan las distintas aceleraciones? Nos dicen que la soga tiene una característica, es inextensible, ¿qué significa esto?

Significa que la distancia entre cualquier par de puntos de la soga (p y q por ejemplo) siempre es la misma, permanece constante (no se estira no se comprime), esto lo escribimos así

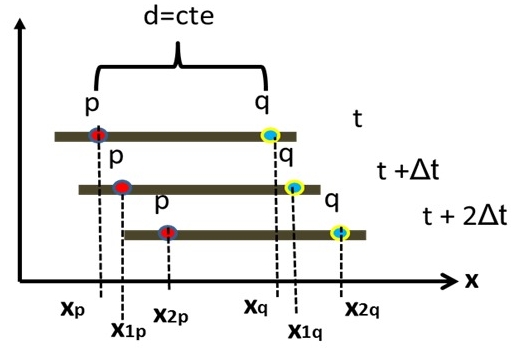  |x_q-x_p| = d= constante

Observemos el gráfico de la izquierda: Para poder entender cuáles son las consecuencia de pedir que la soga es inextensible, simplificamos el estudio al eje x( podría ser cualesquiera); entonces directamente  

 d= x_q-x_p     y se cumple además       

d= x_1q-x_1p            d= x_2q-x_2p

Entonces:

             x_q-x_p      =          x_1q-x_1p             si divido ambas lados de la igualdad por Δt obtengo

    (x_q - x_p) /   Δt   =         (x_1q-x_1p)  /   Δt       distribuyo dentro de cada paréntesis

 x_q/ Δt  - x_p /  Δt   =       x_1q / Δt -  x_1p  /  Δt       

Junto del mismo lado los términos  que describen el mismo punto

x_1p /  Δt  -  x_p /  Δt     =    x_1q / Δt  -   x_q/ Δt  

           (x_1p-x_p   ) / Δt  =  (x_1q-x_q ) / Δt  -->   v_{p media} = v_{q media}  --> lím _(Δt->0) -->   v_p  = v_q   

Esto quiere decir que si la soga es inextensible TODOS sus puntos se mueven con IGUAL velocidad.

Les dejo a Uds.  realizar una deducción similar para averiguar que

a_p  = a_q

Una  soga es inextensible TODOS sus puntos se mueven con IGUAL velocidad y  aceleración.

5) Por lo tanto en el  ejercicio:

                                       a_Ay  = a_Sy = a_By  = a 

6) Con estas consideraciones reescribamos las ecuaciones (I) (II) y (III)

Cuerpo A)   eje y)  F -   F_AS   - P_A = m_A  a     (I)

Cuerpo S)   eje y)  F_AS - F_SB   - P_s = m_s  a     (II)

Cuerpo B)   eje y)          F_SB   - P_B = m_B  a      (III)

Ahora si el número de incógnitas (subrayadas) coincide con el número de ecuaciones y sólo nos queda resolver algebraicamente:

7) (i)La forma de resolver  este sistema lde ecuaciones la eligen Uds. Yo en general utilizo esta :

         Sumo los tres miembros de la derecha, e igualo , a la suma de los tres miembros de la izquierda: 

(F -   F_AS   - P_A  ) + (F_AS - F_SB   - P_s  )+ (F_SB   - P_B )  = m_A  a  +   m_S  a     + m_B  a     

(ii) Observen  que los términos F_AS  se cancelan porque están sumando y restando, ídem con F_SB.

(iii) Por otra parte del lado derecho podemos sacar a factor común, y nos queda la siguiente ecuación:

F - P_A   - P_s  - P_B   =    (m_A   +   m_S   + m_B)  a      -->  a =   (F - P_A   - P_s  - P_B  ) / (m_A + m_S + m_B)  

8) Datos : m_A = 5 kg ;  m_B = 3 kg  ; m_s = 5 g    y |F| = 1000kgf

  (i) -> a =  (1000N –50 N –30N – 0,05N)  /  (5+3+0.005) kg

a=   919,95 N / (8,005) kg     =  114,922   m/s2     

 (ii) A partir de este resultado reemplazamos en (I), (II), (III) y obtenemos las distintas fuerzas:

F_AS   = 375,39  N       y  F_SB  =  374,77 N

Observen que difieren muy poquito esto se debe a que la masa de la soga es muy pequeña.

9) ¿Qué sucede si la masa de la soga tiende a 0?  (  Ps --> 0)

La ecuación (II)   F_AS - F_SB   - P_s = m_s  a   -->   II )   F_AS - F_SB   = m_s  a   = 0 

                                                        F_AS = F_SB     

10) Como las sogas no pueden empujar y siempre están TENSAS en general denominamos a las fuerzas ejercidas por una soga TENSIÓN .Ojo  la soga está  en movimiento, está acelerada.

11) Los nuevos valores son (m_s-->0):  a = 920N/8kg = 115 m/s2 y F_AS = F_SB    = 375N

Nuestras sogas tendrán de ahora en adelante características especiales: serán hilos muy delgados de masa pequeña (despreciable) e inextensibles, y las denominaremos sogas ideales.  

Las  sogas transmiten  la misma fuerza, en el módulo, a lo largo de ella