FISICA | BENDER | AVELLANEDA| Ma-Vi 7 a 23 | 2C 2025
Perfilado de sección
-
MOVIMIENTO CIRCULAR

¿Qué es el movimiento circular?
Un movimiento circular es un movimiento cualquiera en el que su trayectoria es una circunferencia
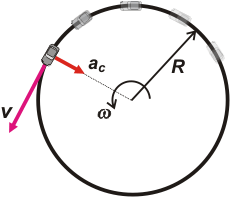
Y es uniforme si el módulo de la velocidad se mantiene constante (está claro que la dirección debe cambiar necesariamente).
Como los desplazamientos son curvilíneos (circunferencias o arcos de circunferencia) suelen denominarse arco recorrido, y simbolizarse Δs, en lugar de Δx o Δy. Luego, la velocidad real (que en este capítulo llamaremos habitualmente velocidad tangencial) será:
v = Δs / Δt
La diferencia fundamental entre arco recorrido y desplazamiento es que Δs se mide sobre la curva (y no punto a punto por un segmento recto).
La variación de ángulo (en la jerga: ángulo barrido), se simboliza ΔΘ. Y la velocidad angular, ω:
ω = ΔΘ / Δt
Cuando el movimiento circular es uniforme (MCU) se verifica que tanto su velocidad angular como su velocidad tangencial conservan su modulo y se cumple que ω = vR
La velocidad no sólo va cambiando de dirección sino también de módulo, y esa variación, para colmo, no es constante. La velocidad del MC es siempre tangente a la trayectoria pero puedo suceder que esta además de variar en dirección también varíen en su modulo
Acá la representé en la velocidad en dos instantes ....
Esta propiedad de que la velocidad varie en modulo y dirección hará que haya dos aceleraciones .. una centrípeta responsable del cambio de dirección y otra tangencial responsable de cambio de "modulo
Vectores en el movimiento Circular
elegir el radio de la trayectoria con \( R \) elegir la posición angular inicial con \( \theta_{0} \)
elegir la velocidad angular inicial con \( \omega_{0} \) para MCUV elegir la aceleración angular con \( \gamma \)
visualizar los vectores en el instante de interés modificando \( t \)
ver en GeoGebra
